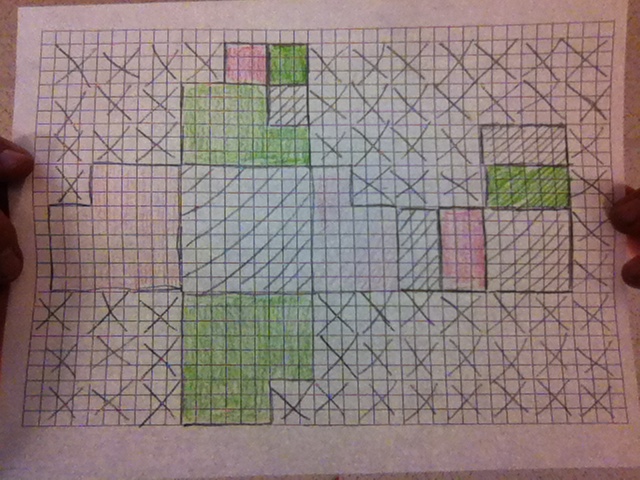
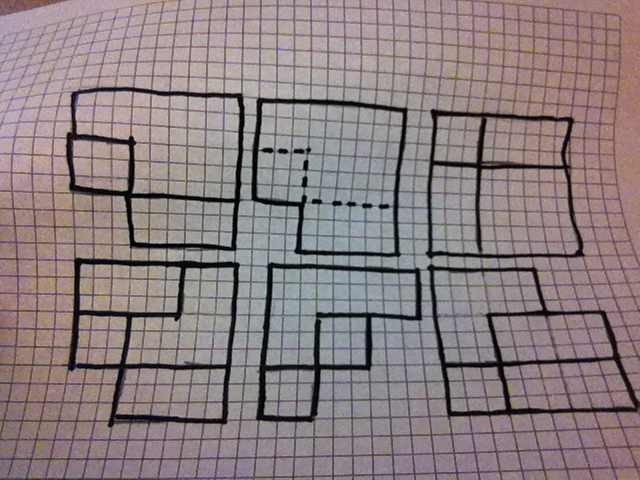
Hexaflexagon

My hexaflexagon used rotational symmetry, most clearly revealed when you rotated the object , because the image on top remained the same. Additionally, also it is rotationally symmetrical because if you fold it over the lines they remain the same. If you look at the pictures to your left, you can see the ideas I am talking about. They are almost exactly the same. Other than the flaws in the coloring, I think that they are quite similar.
My favorite part of the hexaflexagon is that I can flip it over so that it changes. The picture above looks very cool when I flip it around. In retrospect, I would have made some large changes. I would have done some designs that changed when I flipped it. All my designs except for the one above are very boring and I would have changed that.Through this exercise, I learned that I am very easily bored and my work suffers because of it.
Snail Trail Graffiti
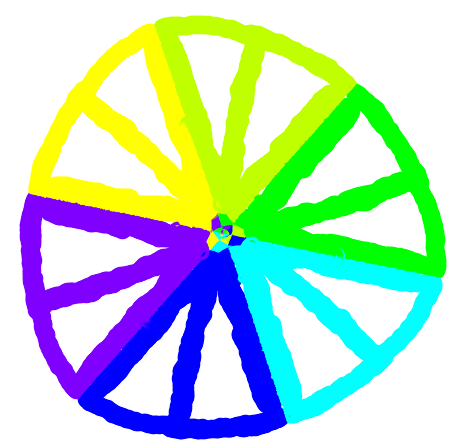
I made the design above by using symmetry. To make the program, my class and I created a wagon wheel out of lines of symmetry. There was a circle with the lines of symmetry for spokes. The lines intersecting the circles created points that all moved when one moved. This meant that when I moved one point, all of them moved. This created beautiful designs. (I was not talking about the wheel above.) The multiple lines of symmetry made it very interesting.
I learned that I look at the world in a three-dimensional way. I learned this because I hadn't thought of this consept in a two-dimensional way, even though it was intriguing. It was good because I want to use this skill.
The Two Rivers
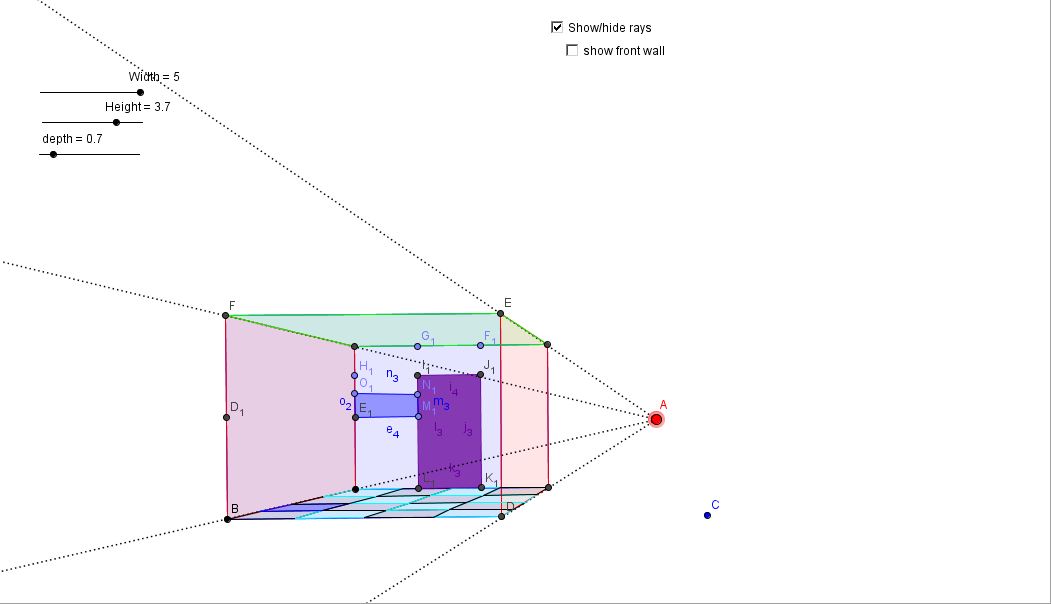
We will model the following scenario in a Geogebra sketch. There is a sewage treatment plant at the
point where two rivers meet. You want to build a house near the two rivers (upstream from the
sewage plant, naturally), but you want the house to be at least 5 miles from the sewage plant. You
visit each of the rivers to go fishing about the same number of times but being lazy, you want to
minimize the amount of walking you do. You want the sum of the distances from your house to the
two rivers to be minimal, that is, the smallest distance.
The big question is this. Where should you build your house? We will use the sketch to model the
scenario and to answer the question.
point where two rivers meet. You want to build a house near the two rivers (upstream from the
sewage plant, naturally), but you want the house to be at least 5 miles from the sewage plant. You
visit each of the rivers to go fishing about the same number of times but being lazy, you want to
minimize the amount of walking you do. You want the sum of the distances from your house to the
two rivers to be minimal, that is, the smallest distance.
The big question is this. Where should you build your house? We will use the sketch to model the
scenario and to answer the question.
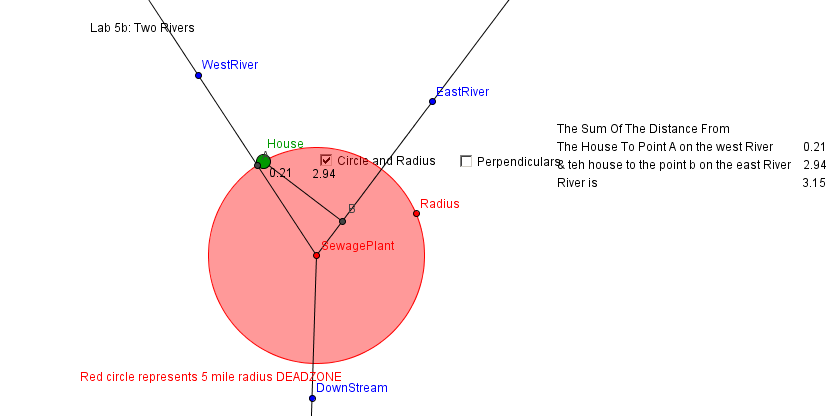
This location was wrong because it had a long walk one day and a short walk the next. This isn’t good because the individual in the story is lazy. This does not work because it is a different walking distance each day. We also can't put it right by both of the two rivers next to the sewage plant because it is poisonous. We want the house in the middle and five miles away, which is represented by the red-circle
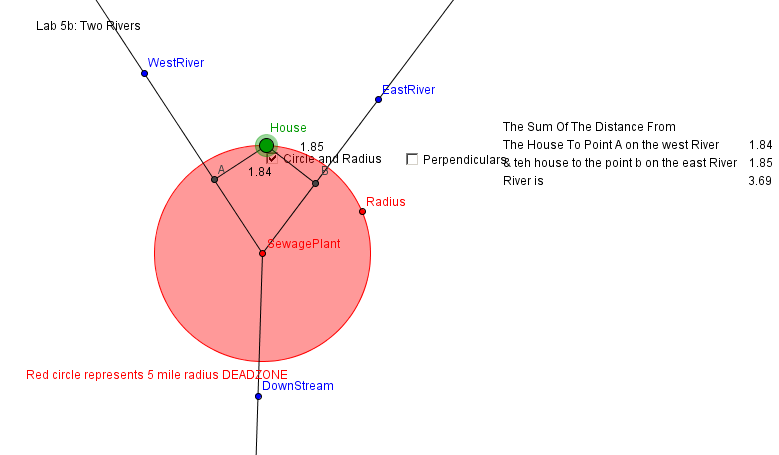
This location is good because the individual is in between the rivers. The walk will be the same both days. It also is the shortest distance we can get. This location works because the distance to both rivers is the same. We also are not in the red circle (the inside of the poison zone). We found the right spot.
In the top photo, we are building the house in the wrong spot. It will be off to one side, making a long walk one day and a short walk the next. The one just above this writing is correct. You will have an equal walk each day. This is perfect!
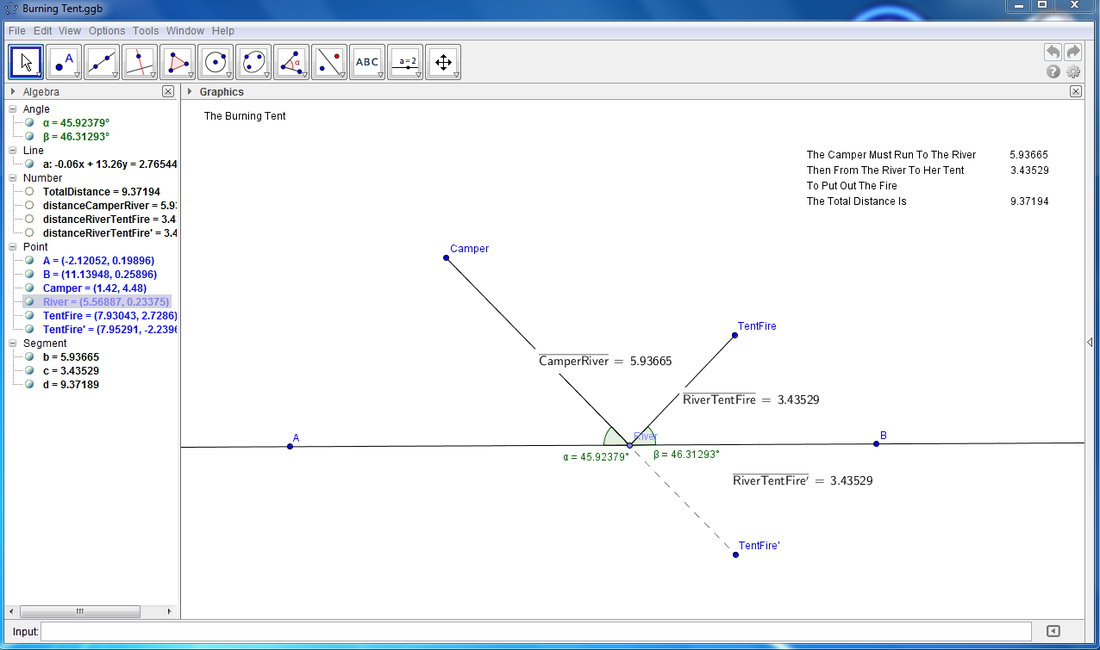
The Burning Tent
A camper out for a hike is returning to her campsite. The shortest
distance between her and her campsite is along a straight line, but as
she approaches her campsite, she sees that her tent is on fire! She must
run to the river to fill her canteen, and then run to her tent to put out
the fire. What is the shortest path she can take? In this exploration you
will investigate the minimal two-part path that goes from a point to a
line and then to another point.
distance between her and her campsite is along a straight line, but as
she approaches her campsite, she sees that her tent is on fire! She must
run to the river to fill her canteen, and then run to her tent to put out
the fire. What is the shortest path she can take? In this exploration you
will investigate the minimal two-part path that goes from a point to a
line and then to another point.
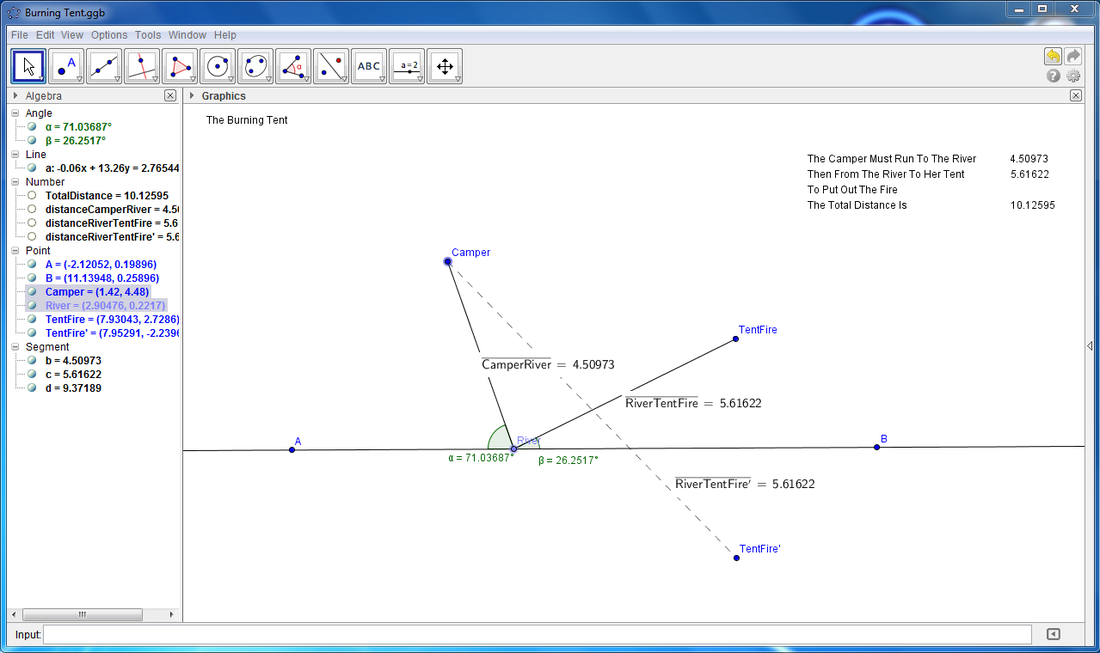
This location isn't any good because the distance to the tent is not as small as it could be. We should run to a different spot. Right now it looks like we need a new tent. This is the wrong spot because we have to turn off the dotted line, the minimum distance. We should go to a different spot.
This is the right spot because it is a straight shot to the ‘TentFire'. This means that it will be a straight shot to the real tent. We will not need to get a new tent. It will work because the line covers up with the dotted line. Currently it will work because we don't turn off the line.
This is the right spot because it is a straight shot to the ‘TentFire'. This means that it will be a straight shot to the real tent. We will not need to get a new tent. It will work because the line covers up with the dotted line. Currently it will work because we don't turn off the line.
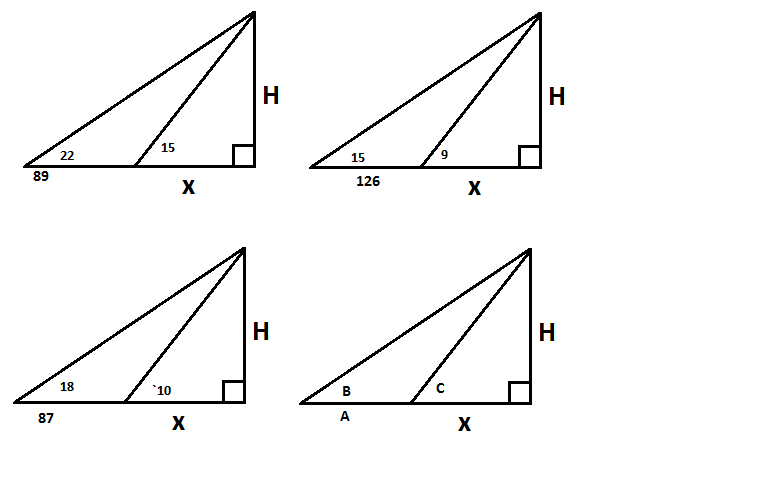
Finding the Height of objects is nature
Equations |
Discription |
|
tan 20=h/w tan 15=H/(89+W)
wtan20= tan15(89+w) wtan20-tan15= 89tan15 w(tan 20-tan15)= 89 tan 15 w = 89 tan 15/(tan20-tan15) |
tan18=h/w tan10=h/(87+w)
wtan18=tan10(87+w) wtan18=87tan10+wtan10 wtan18-wtan10=87tan10 w(tan18-tan10)=87tan10 w=87tan10/(tan18-tan10) |
tan15=h/w tan9=h/(126+w)
wtan15=(126+w)tan9 wtan15=126tan9+wtan9 wtan15-wtan9=126tan9 w(tan15-wtan9)=126tan9 w=126tan9/(tan15-wtan9) |
For an idea of the scenario in real life, please look at the image below. We found an angle, EX- angle a, and then we went 3.56 feet forward, for example. Then we found the other angle, or angle D. Then, with the calculation to the right, we found the height of H.
Picture |
Data Table
West PostEast Telephone PoleSouth Tree |
Angle 120 degrees
18 degrees
15 degrees
|
Angle 215 degrees
10 degrees
9 degrees
|
Distance Between89 ft
87 ft
126 ft
|
My Anamorphic 3-D Drawing Project
Anamorphic means that an image has been projected over an amount of space. This means that the image looks correct from only one perspective. This is a cool effect that shows the amount of perspective that is created in a small space. The definition of anamorphic is an image that is changed because it was projected over a piece of paper. The items I needed were a large piece of paper, a lot of pennies, and a picture frame. To create the projection, my partner and I used a stick to point to a point on the paper that was through the image, which was on the glass. This meant the points were very far from where they would have been if we hadn’t been behind the image. The most challenging part of the product was placing the image on the glass. My group forgot a window/picture frame, so we had to use a lunch container, which was very unhelpful. To conclude, This project was a lot of fun, but still challenging.